Obliczenia dla podziemnych ujęć wodnych

Metody hydrodynamiczne obejmują:

• obliczenia wydajności według wzorów filtracji ustalonej Dupuita na dopływ wody do pojedynczej studni,
• wzory na wielką studnię w przypadku obliczeń wydajności dla zespołu studni,
• obliczenia według wzorów Theisa i Hantusha w przypadku konieczności prognozowania wydajności w warunkach długotrwałej filtracji nieustalonej,
• całkowanie graficzne siatki hydrodynamicznej w przypadku dysponowania mapą hydroizohips.

A. Obliczenia ustalonego dopływu do pojedynczej studni w warstwie nieograniczonej

Studnia o zwierciadle swobodnym

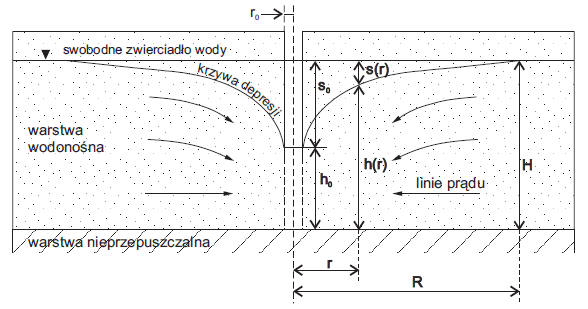
Do obliczeń wydajności przy ustalonej filtracji stosuje się wzory Dupuita.
Dla wód o zwierciadle swobodnym: 

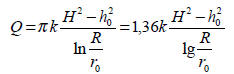
Lub podstawiając za h₀ = H-s

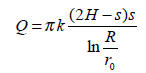
Dla wód o zwierciadle naporowym:

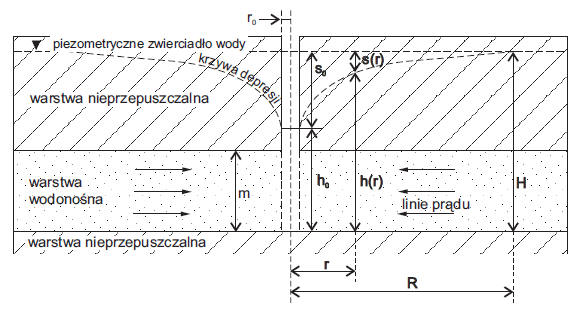
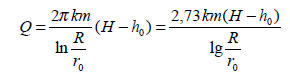
Lub podstawiając H-h₀ = s oraz km = T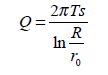

gdzie:
Q – dopływ wody [m3/h],
k – współczynnik filtracji [m/h],
H – wysokość statycznego zwierciadła wody [m],
ho – wysokość dynamicznego zwierciadła wody w studni [m],
s = H – ho depresja zwierciadła wody [m],
m – miąższość warstwy wodonośnej [m],
R – promień leja depresji [m],
ro – promień studni [m].

Zasięg promienia leja depresji oblicza się orientacyjnie za pomocą wzorów empirycznych:

– dla wód o zwierciadle swobodnym według wzoru Kusakina

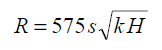
– dla wód o zwierciadle napiętym (naporowym) według wzoru Sichardta: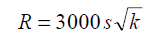Wyniki obliczeń według wzorów empirycznych są zwykle orientacyjne. W związku z tym przy obliczeniach wydajności studni na potrzeby oszacowania zasobów eksploatacyjnych, tam gdzie nie stosowano pompowań hydrowęzłowych, pozwalających na bezpośrednie określenie zasięgu leja depresji pomiarami terenowymi, należy obliczenia empiryczne porówna z przeliczeniem kontrolnym zasięgu leja depresji R jako równoważnego promieniu koła obejmującego swoim zasięgiem obszar zasilania związany ze wstępnie oszacowaną wielkością zasobów eksploatacyjnych.

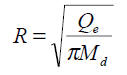
gdzie:
Qe – szacowana wstępnie wielkość zasobów eksploatacyjnych [m3/h],
Md – moduł zasobów odnawialnych przyjęty z hydrogeologicznych badań regionalnych (modelowanie) albo badań hydrologicznych (odpływ podziemny rzek) [m3/h/km2].

W obliczeniach wydajności trzeba odrębnie potraktować przypadki studni, które w swojej konstrukcji nie spełniają założeń przyjętych w schemacie Dupuita i tylko częściowo ujmują daną warstwę wodonośną (są to to tzw.studnie niezupełne) P.  Forchheimer (1930) przedstawił obliczenia odpowiednich poprawek, które wprowadzone do wzorów odnoszących się do studni zupełnych umożliwiają poprawne obliczenia wydajności studni niezupełnych.

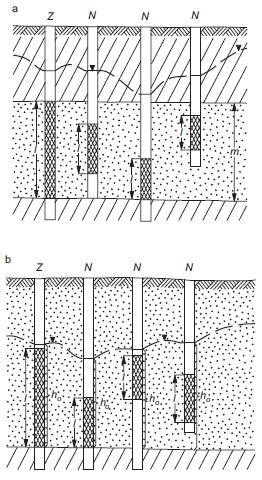
Studnia niezupełna to studnia ujmująca warstwę wodonośną nie na całej jej miąższości lub niecałą miąższość strefy nasycenia, dla której → stopień ujęcia warstwy α < 0,95 , tj. długość części roboczej filtru l jest mniejsza niż miąższość warstwy wodonośnej (m lub h₀). S.n. może być studnią niedogłębioną (wiszącą) lub studnią dogłębioną, w zależności czy filtr właściwy dochodzi do spągu warstwy wodonośnej czy nie.

Przykłady studni niezupełnych a) w warstwie o zwierciadle napiętym, b) w warstwie o zwierciadle swobodnym

Wydajność studni niezupełnej Qn jest wówczas równa:

gdzie:
Q – wydajność studni zupełnej [m3/h],
b – poprawka Forchheimera

Poprawkę Forchheimera określa się z zależności: 

– dla warstwy wodonośnej o zwierciadle swobodnym: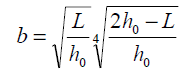

– dla warstwy wodonośnej o zwierciadle naporowym: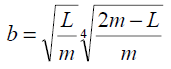

gdzie:
L –  długość części czynnej filtra [m],
h0- wysokość dynamicznego (obniżonego) zwierciadła wody w studni [m],
m – miąższość warstwy wodonośnej [m].

B. Obliczenia dopływu ustalonego do pojedynczej studni w warstwie wodonośnej ograniczonej jednostronnie granicą zasilającą.

Wzory Forchheimera   dla warstwy zasilanej np. z rzeki, której koryto spełnia warunek granicy H=const mają postać:

– dla studni o zwierciadle swobodnym:

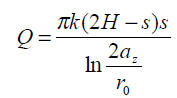
– dla studni o zwierciadle napietym: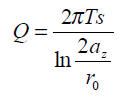

gdzie:
az – odległość studni od granicy zasilającej, pozostałe objaśnienia oznaczeń jak wyżej.

C- obliczanie dopływu ustalonego dla zespołu dwóch studni

Współdziałanie dwóch otworów studziennych ma miejsce, gdy odległość pomiędzy nimi L jest mniejsza niż suma promieni przez nie wytworzonych. Zmniejszenie wydajności studni w warunkach ich współdziałania określa współczynnik interferencji:

gdzie:
Q’ – wydajność studni w warunkach współdziałania,
Q – wydatek studni pracującej indywidualnie.

Schemat współdziałania dwóch otworów studziennych. 1-zwierciadło wody swobodne, 2- krzywe depresji przy pracy tylko jednej lub tylko drugiej studni, 3- krzywa depresji w pompowaniu zespołowym

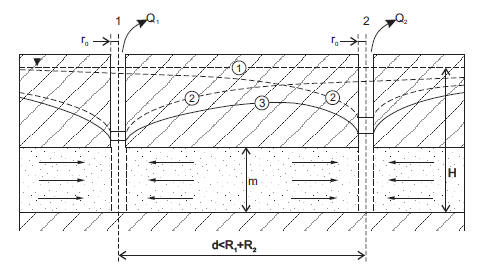
Najczęściej w praktyce współdziałanie zespołu studni liczone jest przy założeniu stałości wydatków poszczególnych studni dla układów:

– dwie studnie współdziałające– wzory Muskata (1937) zmodyfikowane przez A. Haładusa (1983):

a. warstwa wodonośna o zwierciadle swobodnym:

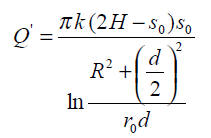
b) warstwa o zwierciadle naporowym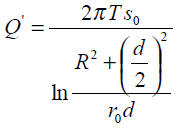

– trzy studnie rozmieszczone w barierze

a. warstwa wodonośna o zwierciadle swobodnym:

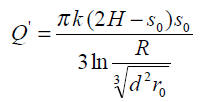
b) warstwa o zwierciadle naporowym

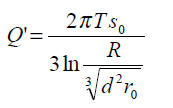
gdzie:
Q – wydajność studni w warunkach jej współdziałania w zespole [m3/h],
T – przewodność warstwy wodonośnej [m2/h],
k współczynnik filtracji [m/h],
H – miąższość warstwy wodonośnej o zwierciadle swobodnym [m],
s₀ – depresja w studni współdziałającej [m],
R – promień leja depresji [m],
d – odległość między sąsiednimi studniami [m],
r₀ – promień studni [m].

D. Obliczenia dopływu ustalonego wody do zespołu otworów metodą wielkiej studni

Metodę wielkiej studni stosuje się w przypadku obliczania zasobów zespołu studni. Metoda polega na wyznaczeniu promienia zastępczego r_k a następnie wprowadzenia jego wartości do przytoczonych powyżej wzorów Dupuita.

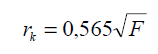
Dla ujęcia (w warstwie nieograniczonej) o długości nie przekraczającej 3-4-krotnie jego szerokości można również stosować metodę wielkiej studni, obliczając promień zastępczy wzorem podanym przez Bindemanna i Jazwina.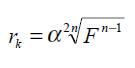
gdzie:
F – pole powierzchni ujęcia ograniczone najbliższą hydroizohipsą
n – liczba studni ujęcia,
α – współczynnik korygujący

Wartość współczynnika α

źródło:
1) www.instsani.pl